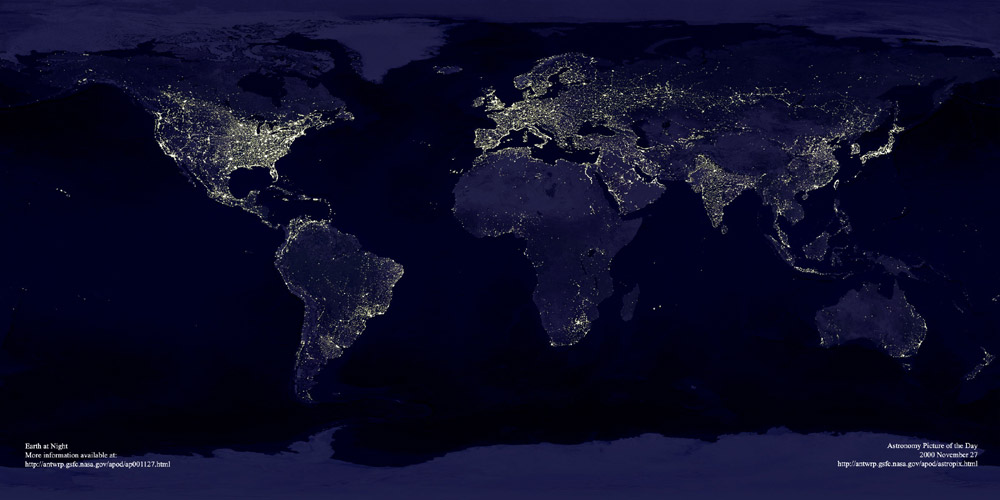
I've wondered for a while about how far away we could see the earth if we were using our current technology and we had our current light output. At what distance could we see the artificial light the earth produced?
This paper Detection Technique for Artificially-Illuminated Objects in the Outer Solar System and Beyond provides some sort of evidence on the question
Existing optical telescopes and surveys can detect artificially illuminated objects comparable in total brightness to a major terrestrial city at the outskirts of the Solar System
...
For this signature to be detectable, the night side needs to have an artificial brightness comparable to the natural illumination of the day side. Clearly, the corresponding extraterrestrial civilization would need to employ much brighter and more extensive artificial lighting than we do currently since the global contrast between the day and night sides is a factor ∼ 6 × 10^5 for the present-day Earth
Lets ignore that our telescopes will get better (about 2.5% a year?) so how quickly at current rates will the earth take to be this bright?
“over the last three centuries, and even now, the world spends about 0.72% of its GDP on light. This was the case in the UK in 1700 (UK 1700), is the case in the undeveloped world not on grid electricity in modern times, and is the case for the developed world in modern times using the most advanced lighting technologies.”
But what is that in terms of extra light produced? "In 1700 a typical Briton consumed 580 lumen-hours in the course of a year, from candles, wood and oil. Today, burning electric lights, he uses about 46 megalumen-hours—almost 100,000 times as much."
So that means if we grew at the same rate we have for the last 300 in about 300 years we will be producing enough light that if it was all shone out into space the earth would be as bright at night to an outside observer as it is in the day. I dont think you can make projections this far and it still leaves the question of how long after that ambient external light would be that bright. Still I think its interesting that even with current detection technology as civilisation the 300 years advanced from us would be nearly visible to us. I would guess this prediction will reduce but 300 years is my first estimate to when we could see ourselves.
5 comments:
Start here:
http://www.bautforum.com/archive/index.php/t-47335.html
Absolute magnitude of the earth=-4
Now I suspect this is high due to the phase issues mentioned:
http://en.wikipedia.org/wiki/Absolute_magnitude
Then given the HST observable apparent magnitude:
http://en.wikipedia.org/wiki/Apparent_magnitude
of -31, and the distance modulus:
http://en.wikipedia.org/wiki/Distance_modulus
we get ~1000 parsec.
Presumable this is anisotropic wrt absorption by interstellar dust.
As you say, growth in telescope size and sensitivity of detectors will be a factor as to how this changes.
I suppose the real challenge is the differential between the Sun and the earth (~30 degrees of magnitude in brightness) at a separation of 2e-6 degrees at 1k parsec, which may well reduce the distance.
Great comment!
Back of the envelope 1000 parsecs is more than a billion stars. Which means if life like us was common you would expect to see it?
Probably not given the distance of those extrasolar planets thus detected:
http://en.wikipedia.org/wiki/List_of_extrasolar_planets
http://en.wikipedia.org/wiki/Extrasolar_planet#Number_of_stars_with_planets
Ed Turner has been working on similar (simplistic) ideas for a few years now.
At the moment, brightness is not the issue so much as contrast. Jupiter has an absolute magnitude of about 19, so I'm guessing the earth is probably about 25 or thereabouts (not -4 as Gonecaving says, that's way too bright). HST has gone as faint as apparent magnitude of 31, so Earth brightness objects are already detectable at reasonable distances.
The trouble with finding planets is that they get lost in the glare of their parent star. An alien astronomer, 10 parsecs away would need to be able to cancel out all but one part in 10^10 of the sun's light within a disc only 0.1 arcsec wide to be able to detect Earthshine. Our current technology routines achieves one part in 10^4.
I haven't read the paper, so I can't comment on the power law argument, but it would worry me that the lights at night would tend to even out the day-night contrast (which is , making it harder to figure out what was going on down on the planet surface.
Thanks Fergal
How does the inverse square law effect this? If telescopes are getting 2.% better per year. And gdp is growing 2% per year and light is a set % of GDP. And light efficiency is growing x% per year. You cannot just add up the percentages to say how our visible radius is expanding you'd have to take the inverse square law into account?
Post a Comment